Generic selectors
Exact matches only
Search in title
Search in content
Post Type Selectors
Contact Us

 

 

The Collatz Conjecture

An elegant math problem that inspires lovely visuals and lively holiday conversation.

RSG Simple Divider

What is the Collatz Conjecture?

The Collatz Conjecture (also known as the 3 n + 1 problem, the Ulam conjecture, or the Hailstone problem) was introduced by Lothar Collatz in 1939. The conjecture starts with a process: 

  • Choose any number.

  • If it is even, divide it by 2.

  • If it is odd, multiply it by 3 and then add 1.

  • Repeat with the new number.

For example:

Screen Shot 2019-10-10 at 12.30.16 PM

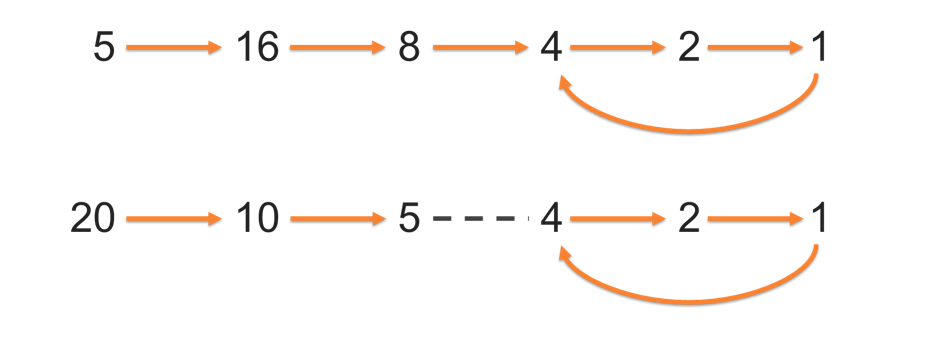
The conjecture states no matter what number you start with, you will 'always' get to the 4-2-1 cycle. Interesting, right? Computers have checked up to 87*260, but currently there is no formal proof that you always get to 1. 

So how about those funky visuals?

Such an interesting and complex pattern of numbers begs to be shown as a visual. That is just what RSG's Senior Data Scientist Jeff Dumont set out to do. But, Jeff was interested in what the Collatz Conjecture looks like with non-natural numbers like 2.5 (is it odd or even?), pi, and the square root of -1. Here's what they look like:

Screen Shot 2019-10-10 at 12.48.36 PM

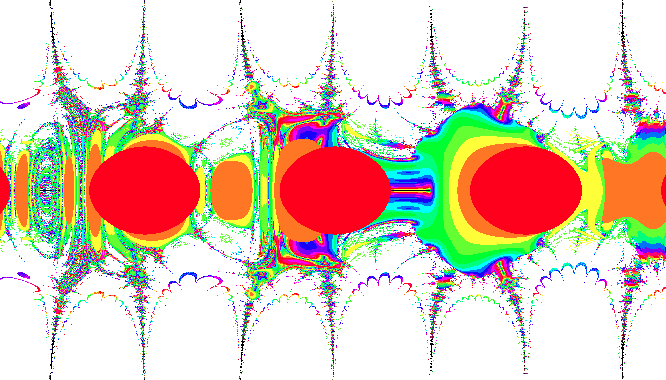
Here Jeff shows results for numbers near 0 in the complex plane (i.e., the surface of real and imaginary numbers). The colors correspond with how quickly the Collatz process returns to the 4-2-1 cycle (i.e., the length of the series) with red moving quicker than orange, orange quicker than yellow, etc.

esc_1z12

 

 

The beauty of the Collatz problem can be explored by zooming in on some of the tendrils that appear in the previous figure. By zooming in we see some intricate "fingers" of behavior that are quite complex and unexpected.

Screen Shot 2019-10-10 at 12.48.06 PM

 

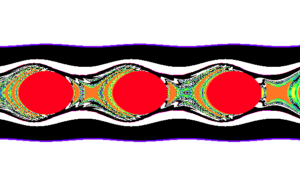
There are a number of ways to determine odd or even in the Collatz process. Here Jeff explores an alternative approach which results in a different pattern. It is similarly intricate and intriguing.

Jeff shared this work in a recent company-wide RSG seminar. We hold these each Wednesday to share interesting project work and personal passions. If you're intrigued and want to learn more about these visualizations, reach out to Jeff. Like many of us, he loves math and sharing its beauty and power with others.

Looking for things to talk about during the holidays?

Whether you are talking with your astrophysicist aunt or 4th grade nephew, you can dazzle them with The Collatz Conjecture. Try asking them:

  • Can you believe that they've never been able to prove this?

  • Which visual pattern do you like the most and why?

  • Can you beat me to the 4-2-1 sequence when starting with the number 33? (no calculators allowed)

  • What's your favorite math problem?

  • What's the greater meaning of this numeric pattern?

 

Jeffrey P. Dumont and Clifford A. Reiter, Real Dynamics Of A 3-Power Extension Of The 3x+1 Function, Dynamics of Continuous, Discrete and Impulsive Systems: A Mathematical Analysis, 10 (2003) 875-893

Jeffrey P. Dumont and Clifford A. Reiter, Visualizing Generalized 3x+1 Function Dynamics, Computers & Graphics, 25 5 (2001) 883-898